串联RLC电路由一个电阻、一个电容和一个电感串联在一个交流电源上

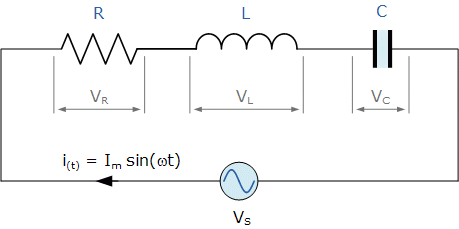
到目前为止，我们已经看到三个基本的被动组件：抵抗 ,电感，和电容当连接到正弦交流电源时，彼此的相位关系非常不同。

在纯欧姆电阻器中，电压波形与电流“同相”。在纯电感中，电压波形“领先”电流90o，给我们的表达式是：伊莱。在纯电容中，电压波形“滞后”电流90o冰给我们的表情

这个相位差，Φ取决于所用元件的无功值，希望现在我们知道电抗(十)如果电路元件是电阻元件，则为零；如果电路元件是感性元件，则为正；如果电路元件是电容性元件，则为负，因此产生的阻抗为：

电路元件	电阻（R）	电抗，（X）	阻抗，（Z）
电阻器	R	0
电感器	0	0
电容器	0	1/wc

我们可以把这三个无源元件组合成一个串联的RLC电路，而不是分别分析每个无源元件。a的分析串联RLC电路与双系列相同R我和RC我们之前看过的电路，这次我们需要考虑两者的大小十我和十C求出整个电路的电抗。串联RLC电路被归类为二阶电路，因为它们包含两个储能元件，一个电感我还有一个电容C. 考虑下面的RLC电路。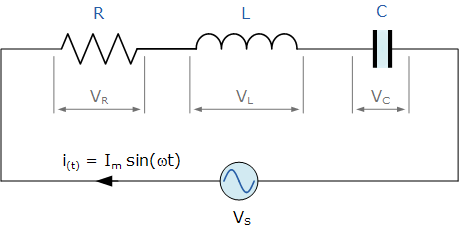

上面的串联RLC电路有一个单回路，流过回路的瞬时电流对每个电路元件都是相同的。因为电感和电容的电抗十我和十C是电源频率的函数，因此串联RLC电路的正弦响应将随频率变化，E. 然后每个电路元件的电压下降R ,我和C元件将彼此“异相”，定义如下：

• i（t）=Imaxsin（ωt）

• 纯电阻上的瞬时电压与电流“同相”

• 通过一个纯电感器的瞬时电压，VL“领先”电流90度

• 通过纯电容器的瞬时电压，VC“滞后”电流90度

• 因此，这两个方向是“异相”的，并且相互对立。

对于上面的串联RLC电路，可以表示为：

串联RLC电路中所有三个元件的源电压幅值由三个单独的元件电压组成，VR ,VL和VC与所有三个元件共用的电流。因此，矢量图将以电流矢量为基准，根据该基准绘制三个电压矢量，如下所示。

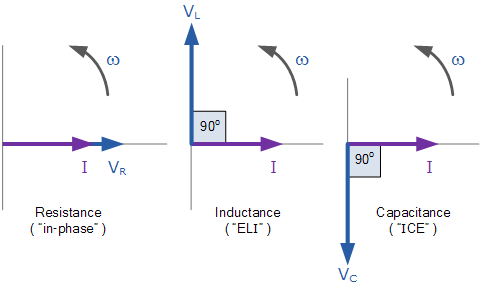
这意味着我们不能简单地相加VR ,VL和VC找到电源电压，VS由于三个电压矢量指向电流矢量的不同方向，所以在所有三个分量上。因此我们必须找到电源电压，VS作为相量和三个分量的电压矢量组合在一起。

回路和节点电路的基尔霍夫电压定律（KVL）指出，在任何闭合回路周围，回路周围的电压降之和等于电动势之和。然后将这一定律应用于这三个电压，我们将得到源电压的振幅，VS作为

串联RLC电路的相量图是通过将上述三个单独的相量组合在一起并以矢量方式添加这些电压而得到的。由于流经电路的电流对所有三个电路元件是共用的，因此我们可以将其用作参考矢量，并在相应的角度绘制三个电压矢量。

结果向量VS通过将两个向量相加得到，VL和VC然后把这个和加到剩下的向量上VR. 得到的角度VS和我为电路相角，如下所示。

从上面右手边的相量图可以看出，电压矢量产生一个矩形三角形，由斜边组成VS，水平轴VR和垂直轴VL–VC希望你会注意到，这是我们以前最喜欢的电压三角形因此，我们可以利用这个电压三角形上的毕达哥拉斯定理，从数学上得到VS如图所示

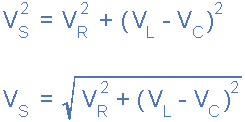
请注意，当使用上述公式时，最终无功电压必须始终为正值，即最小电压必须始终从最大电压中减去，我们不能将负电压加到其中VR所以有VL–VC或VC–VL 从最大值中取最小值，否则计算VS将是不正确的

由上可知，串联RLC电路中所有元件的电流幅值和相位相同。然后，通过每个元件的电压也可以根据流过的电流进行数学描述，并且通过每个元件的电压为。

通过将这些值代入上面的毕达哥拉斯方程中的电压三角形，我们可以得到：

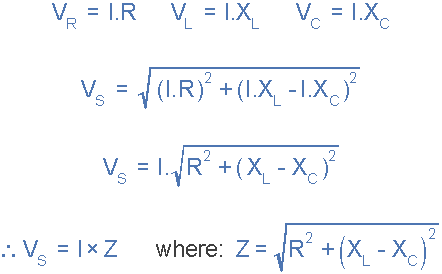
所以我们可以看到，源电压的振幅和流过电路的电流的振幅成正比。这个比例常数称为阻抗最终取决于电阻和电感和电容电抗的电路。

然后在上面的串联RLC电路中，可以看出，对电流的反对是由三个元件组成的，XL ,XC和R有了电抗，XT任何串联RLC电路的定义如下：XT= XL–XC或XT= XC–XL以较大者为准。因此，电路的总阻抗被认为是驱动电流通过它所需的电压源。

由于三个矢量电压不相一致，XL ,XC和R也必须是“异相”与彼此之间的关系R ,XL和XC是这三个分量的向量和。这将给我们RLC电路的整体阻抗，Z. 这些电路阻抗可以用阻抗三角形如下所示

阻抗Z一个串联RLC电路取决于角频率， o也一样十我和十C如果电容电抗大于电感电抗，十C>十我然后整个电路的电抗是电容性的，给出一个超前相位角。

同样，如果感应电抗大于容性电抗，XL;XC然后整个电路的电抗是感性的，给串联电路一个滞后的相角。如果两个电抗相同，并且十我= XC发生这种情况的角频率称为共振频率，并产生共振我们将在另一个教程中详细介绍。

然后电流的大小取决于应用于串联RLC电路的频率。当阻抗，Z在最大值时，电流是最小值，同样，当Z是最小值，电流是最大值。因此，上述阻抗方程可改写为：

相角， d在电源电压之间，五S以及电流，我与Z和R在阻抗三角形中。这个相角的值可以是正的，也可以是负的，这取决于源电压超前还是滞后于电路电流，并且可以根据阻抗三角形的欧姆值进行数学计算，如下所示：

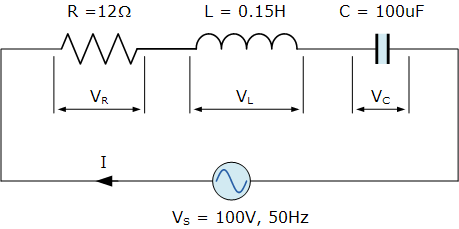
电阻为12Ω、电感为0.15H、电容为100uF的串联RLC电路通过100V、50Hz电源串联。计算电路总阻抗、电路电流、功率因数，绘制电压相量图。

感应电抗，XL .

电容电抗，XC .

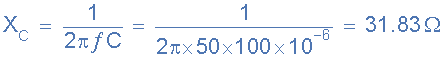
电路阻抗，Z .

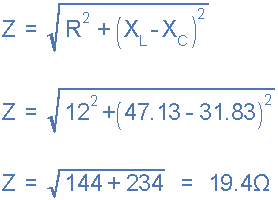
电路电流，我 .

串联RLC电路的电压，VR ,VL ,VC .

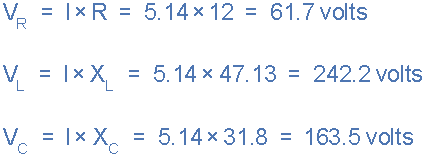
电路功率因数和相角， d .

相量图

因为相角 d计算为正值51.8o电路的总电抗必须是感性的。在串联RLC电路中，我们将电流矢量作为参考矢量，电流“滞后”源电压51.8o所以我们可以说相角是滞后的，正如我们的记忆表达式所证实的那样 "Li" .

在一个串联RLC电路包含一个电阻，一个电感器和一个电容器源电压五S相量和由三个分量组成，五R ,五我和五C三对三都是共同的。由于电流对所有三个元件都是公共的，所以在构造电压三角形时，它被用作水平参考。

电路的阻抗等于电流的总阻力。对于串联RLC电路，可以通过将电压三角形的每边除以其电流来绘制阻抗三角形，我. 电阻元件上的电压降等于I*R公司，两个无功元件之间的电压为I*X = I*XL–I*XC而源电压等于I*Z. 夹角VS和L是相角， d .

当使用含有多个电阻、电容或电感的串联RLC电路时，它们可以全部加在一起形成一个单独的元件。例如，所有电阻相加，RT= ( R1 R2 R3 )…等等或者所有的电感我T= ( L1 L2 L3 )……等这样，一个含有许多元件的电路可以很容易地简化为一个单一的阻抗。

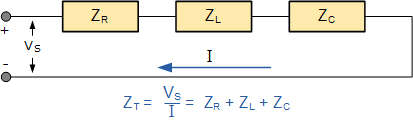
在下一个关于并联RLC电路的教程中，我们将研究在并联电路配置中，当应用稳态正弦交流波形以及相应的相量图表示时，三个元件连接在一起的电压-电流关系。我们还将介绍导纳第一次

*博客内容为网友个人发布，仅代表博主个人观点，如有侵权请联系工作人员删除。