正弦波形的有效值或有效值与等效直流电源的加热效果相同

在我们关于交流波形我们简单地看了一下均方根电压一个正弦波形的值，并且说这个RMS值产生了与等效直流功率相同的热效应，在本教程中，我们将通过更详细地研究RMS电压和电流来进一步扩展这个理论。

术语“RMS”代表“均方根”。大多数书籍将其定义为“产生与等效直流电相同的加热效果的交流功率的量”，或者类似的东西，但是RMS值不仅仅是这样。均方根值是瞬时值平方函数的平均值（平均值）的平方根。用于定义RMS值的符号有五有效值或我有效值 .

术语RMS，仅指时变正弦电压、电流或复杂波形的幅值随时间的变化而变化，在直流电路分析或计算中不使用幅值总是恒定的。当用于比较交流正弦波形的等效均方根电压值时，该正弦波形向给定负载提供与等效直流电路相同的电能，则有效值被称为“有效值”，通常表示为：五 有效或我 有效 .

换句话说，有效值是一个等效的直流值，它告诉你一个时变正弦波形产生相同功率的能力等于多少伏或多少安培的直流电。

例如，英国的国内电源是240Vac。假定该值表示“240伏rms”的有效值。这意味着英国家庭墙上插座的正弦均方根电压能够产生与240伏稳定直流电压相同的平均正功率，如下所示。

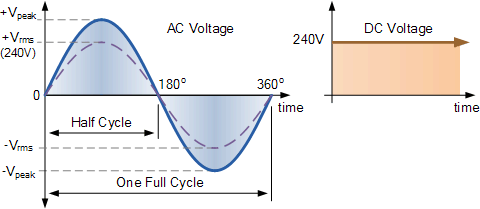
那么我们如何计算均方根电压正弦波形的。正弦波或复波形的均方根电压可用两种基本方法确定。

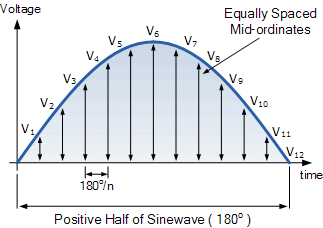
• 图解法–通过在波形上绘制多个中间坐标，可用于找到任何非正弦时变波形的均方根值。

• 分析方法–是一种使用微积分求任何周期性电压或电流的有效值或均方根值的数学程序。

虽然计算方法对于交流波形的两半是相同的，但在本例中，我们将只考虑正半周。通过取波形的有效值或有效值，可以找到波形的有效值。

波形的正半部分被分成任意数量的“n”等分，或中纵坐标沿着波形绘制的中间坐标越多，最终结果就越精确。因此，每个中间纵坐标的宽度为no每个中间纵坐标的度数和高度将等于当时波形沿波形x轴的瞬时值。

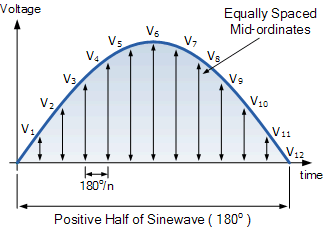
波形的每个中间纵坐标值（在本例中为电压波形）乘以其本身（平方）并加到下一个值上。这个方法给出了“平方”或方形RMS电压表达式的一部分。接下来，这个平方值除以用来计算中庸RMS电压表达式的一部分，在我们上面的简单例子中，使用的中间坐标数是十二（12）。最后，发现前面的结果的平方根可以给出根有效值电压的一部分

然后我们可以定义用来描述均方根电压（V有效值)作为“广场”根的意思是的广场电压波形的中间纵坐标”，其表示为：

对于上面的简单示例，RMS电压的计算公式如下：

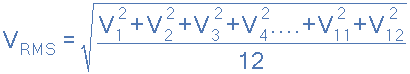
假设交流电压有峰值电压(五pk键)通过取10个中间坐标值，发现在一个半周期内变化如下：

这个均方根电压因此计算如下：

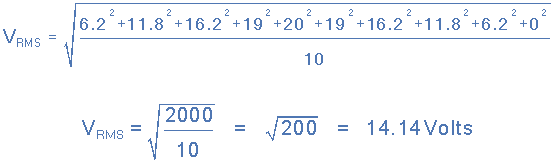
然后，使用图解法得出的均方根电压值如下： 14.14伏 .

上面的图解法是一种很好的方法，可以求出非对称或正弦的交流波形的有效电压或有效值（或电流）。换句话说，波形形状类似于复杂波形。然而，当处理纯正弦波形时，我们可以通过分析或数学的方法来找到均方根值，从而使我们的生活更轻松一些。

周期性正弦电压是恒定的，可以定义为五（吨）= V最大值 *cos（ωt）有一段时间T. 然后我们可以计算均方根正弦电压（V）的（rms）值（吨）)作为：

从0到360的极限积分o或“T”，句点给出：

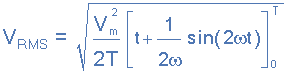
哪里：虚拟机是波形的峰值或最大值。进一步划分为ω = 2π/T，上面的复杂方程最终也会减少：

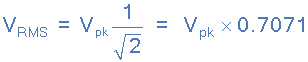
然后是RMS电压(五有效值)通过峰值电压乘以0.7071，等于1除以2的平方根(1/√2).. 均方根电压也可以称为有效值，它取决于波形的大小，而不是波形频率或相位角的函数。

从上面的图形示例来看，峰值电压(五pk键)其波形为20伏。通过使用刚刚定义的分析方法，我们可以计算RMS电压如下：

VRMS= Vpk* 0.7071 = 20 x 0.7071 = 14.14V

注意这个值 14.14伏与上一个图形方法的值相同。然后我们可以使用中间坐标图解法或解析计算法来求出正弦波形的均方根电压或电流值。

请注意，将峰值或最大值乘以常数 zero point seven zero seven one ,只有适用于正弦波形。对于非正弦波形，必须使用图解法。

除了使用正弦波的峰值或最大值，我们还可以使用峰-峰（VP-P公司)值或平均值（V 平均)求正弦波等效均方根值的值，如下所示：

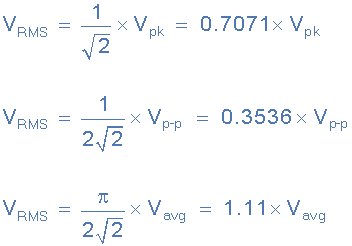
然后进行总结。在处理交流电压（或电流）时，我们面临的问题是如何表示电压或信号量。一种简单的方法是使用波形的峰值。另一种常见的方法是使用有效值，有效值也可以通过更常见的均方根或者简单的RMS值

正弦曲线的均方根、均方根值与所有瞬时值的平均值不同。电压均方根值与电压最大值之比等于电流均方根值与电流最大值之比。

大多数万用表，无论是电压表还是电流表，都假设是纯正弦波形来测量均方根值。为求非正弦波形的均方根值，需要“真有效值万用表”。

正弦波形的RMS值与相同值的直流电流具有相同的加热效果。如果直流电，我通过的阻力R欧姆因此，电阻作为热量消耗的直流功率我 twoR瓦茨。如果是交流电，i = I最大值 *合成通过相同的电阻，交流功率转换成热量将是：我 two有效值*R瓦茨

当处理交流电压和电流时，除非另有说明，否则应将其视为均方根值。因此，10安培的交流电与10安培的直流电具有相同的加热效果，最大值为14.14安培。

现在已经确定了交流电压（或电流）波形的RMS值，在下一个教程中，我们将研究如何计算平均值，五 平均最后比较两者

*博客内容为网友个人发布，仅代表博主个人观点，如有侵权请联系工作人员删除。