当能量通过电场从一个电路耦合到另一个电路时，就会发生电场耦合（也称为电容耦合）。正如我们将看到的，当源电路的阻抗很高时，这种情况最有可能发生。

考虑两个电路共用一个公共回路平面，如图1所示。如果回路平面的电阻为零，则公共阻抗耦合为零。然而，由于从一条信号线开始，在另一条信号线上终止的电场线也可能在两个电路之间发生耦合。例如，如果其中一个信号电压为1V，另一个信号电压为0V，则两条信号线之间的电位差会导致电场线从1V导线开始，在0V导线上终止。从原理上讲，这可以用两条信号线之间的电容来表示。

当然，还有其他的电场线从1V导线开始，在0V平面上终止。这可以用导线和平面之间的电容来表示。图2示出了图1中包括电场耦合电容的两个电路的示意图。

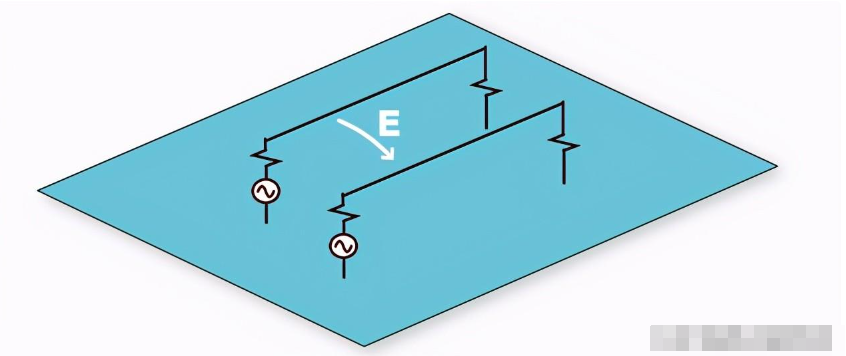
图1：信号返回平面上方的两个电路。

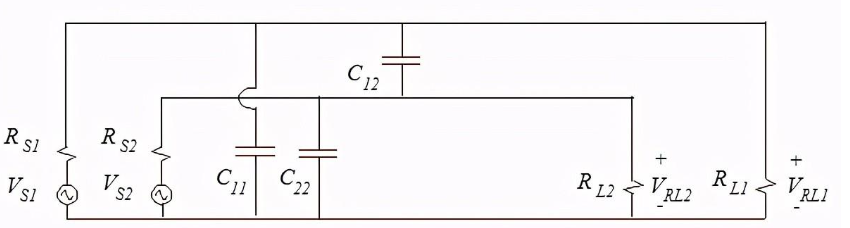
图2：图1中包括电容耦合路径的电路示意图。

在这种情况下，导线之间的电容C12很容易用两条导线之间的电容公式计算，电容c11和c22可以用接地层上方导线的电容公式计算。一旦确定了电容，并且将值分配给图2中的所有元件，就可以使用用于公共阻抗耦合的相同基本公式来计算由于电场耦合而产生的串扰，

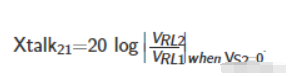
如果我们试图找到精确的解决方案，分析这个电路与9个元素的过程可能会很费时。然而，如果我们重新绘制电路，并利用一些阻抗的相对大小，我们可以大大简化分析。

首先，让我们重新绘制图2中的电路，如图3所示。通过将电路1放在示意图的左侧，将电路2放在右侧，重要的耦合C12就更清晰了。此外，认识到自电容C11和C22的阻抗几乎总是比它们并联的负载阻抗高得多也是有帮助的。如果这不是真的，到达负载的信号将显著衰减。因此，在求解图3中的电路时，我们通常可以忽略C11和C22。

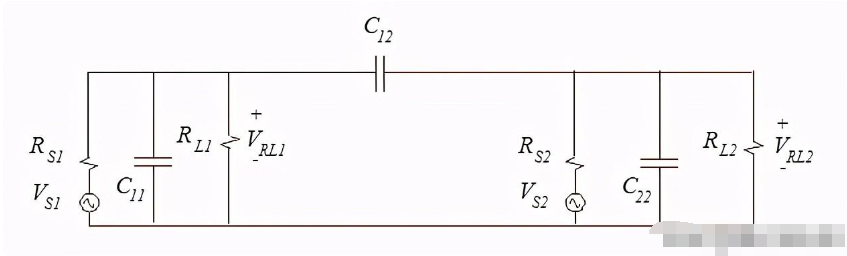
图3：图1中电路的更直观的示意图。

为了计算由电路1中的信号引起的电路2中的串扰，我们设置vs2=0并确定比率vrl2/VRL1。如果耦合相对较弱（即，如果耦合没有向下加载源电路），则C12的阻抗相对于电路1中的阻抗较大。这意味着VRL1的值与电路2的参数无关，电路可以用图4所示的简单形式表示。

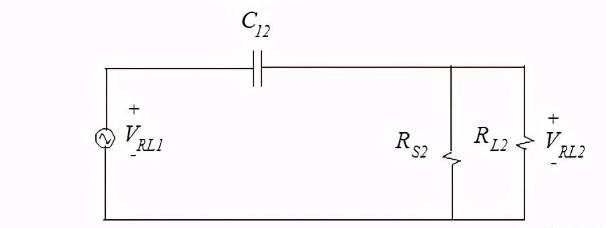
图4：图1中电路的更简单的表示。

现在这个电路比较容易解决。串扰可以表示为，

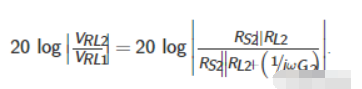
方程2

对于图1和图2中的电路，假设信号线高出导电平面4.0 mm，长16 cm。假设导线半径为0.8 mm，导线之间的间距为3.0 mm。设RS1=RS2=10欧姆，RL1=RL2=150欧姆。计算这些电路在50mhz时由于电场耦合而产生的串扰。

我们首先确定电容C11、C22和C12。平面上每根导线的电容约为，

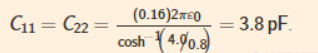
方程3

两根导线之间的电容大约为，

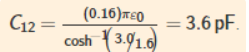
方程4

C11和C22在50 MHz时的阻抗为| 1/jΩC |=800欧姆。由于这远高于150欧姆的电路阻抗，我们可以忽略这些电容。耦合电容的阻抗为| 1/jΩC |=890欧姆。这也比电路阻抗大得多，因此我们可以用方程（2）来计算串扰，

方程5

在这种情况下，注意改变各种电路参数将如何改变耦合是很有帮助的。例如，加倍频率会加倍串扰（即，在100 MHz时，计算的串扰为-34 dB）。对于弱耦合情况，电场耦合与频率成正比。

在本例中，将受害电路的源电阻加倍也会使串扰加倍。注意，源电阻和负载电阻的并联组合几乎等于源电阻。在本例中，将负载电阻加倍对串扰影响不大，因为重要的是受害电路中源电阻和负载电阻的并联组合。

本例中的另一个重要参数是互电容C12。减小C12的值将成比例地减小串扰。将导线移动得更远是减小C12值的一种方法。但是，需要注意的是，仅将导线之间的距离加倍不足以将12减少2倍。当导线间距大于导线直径时，反双曲余弦函数的行为类似于对数函数。在这种情况下，将导线之间的距离加倍（从3.0 mm增加到6.0 mm）会将C12的值从3.6 pF更改为2.2 pF。这将减少串扰只有约4分贝。

*博客内容为网友个人发布，仅代表博主个人观点，如有侵权请联系工作人员删除。