本系列12篇文章的第5部分继续探讨有效噪声带宽，因为它与delta sigma adc和系统级设计有关，通过一个简单的例子，使用两级滤波器来理解如何计算ENBW以及系统变化如何影响ENBW。

在第四部分在解析信号系列的过程中，我讨论了基本的有效噪声带宽（ENBW）主题，包括ENBW是什么，为什么需要它，以及它来自何处。

在第5部分中，我将继续探讨ENBW，因为它与delta-sigma模数转换器（ADC）和系统级设计有关，通过一个使用两级滤波器的简单示例来了解ENBW的重要方面：

1. 如何计算ENBW

2. 系统变化如何影响ENBW。

对于本例，让我们使用一个简单的两级数据采集系统，该系统由一个抗混叠滤波器和一个δ-西格玛模数转换器使用集成的sinc滤波器，如图1所示。如前所述，我将重点讨论这两种滤波器类型，因为它们通常对整个ENBW的影响最大，但这种分析通常适用于任何类型或数量的附加滤波器。

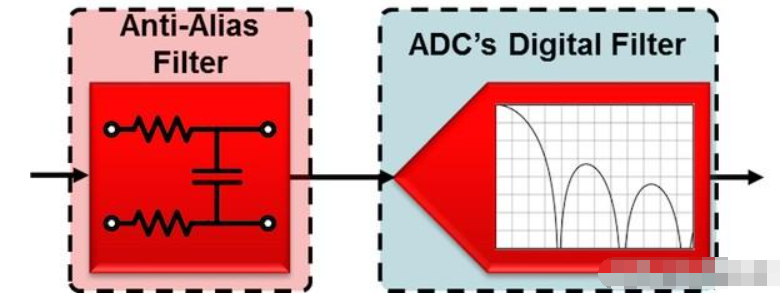
图1简化数据采集系统框图

对于抗混叠滤波器，让我们使用单极电阻电容（RC）滤波器，因为我已经在本系列文章的第4部分讨论了如何计算它的ENBW（在下面的等式1中重申）。此外，delta-sigma ADC通常只需要一个简单的RC滤波器来提供足够的抗混叠。表1总结了本例中选择的电阻和电容值，尽管存在其他有效的组合。

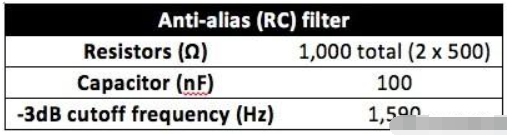
表1抗锯齿过滤器组件值

选择被动分量值后，使用方程式1计算抗混叠滤波器的ENBW：

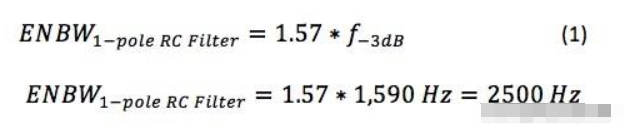
最后，绘制反走样过滤器的响应，如图2所示，过滤器的ENBW用红色阴影区域表示。

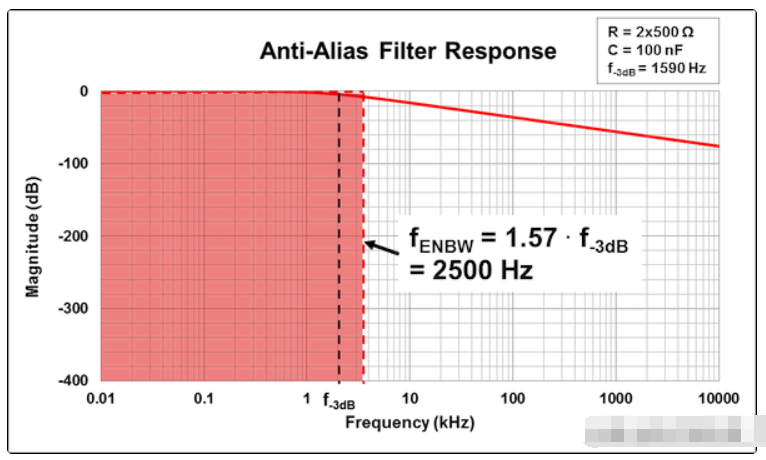
图2 突出显示ENBW的抗混叠滤波器响应

在充分了解抗混叠滤波器的频率响应后，下一步是确定ADC的sinc滤波器的响应。对于本例，让我们选择32位低噪声ADS1262来自德州仪器公司（TI），尽管这种分析通常适用于任何δ-西格玛ADC。在本例中，我将以每秒60个样本（SPS）的数据速率使用ADS1262的sinc4滤波器。图3重新创建了这个过滤器在这些设置下的频率响应的数据表图（从ADS1262配置工具 ).

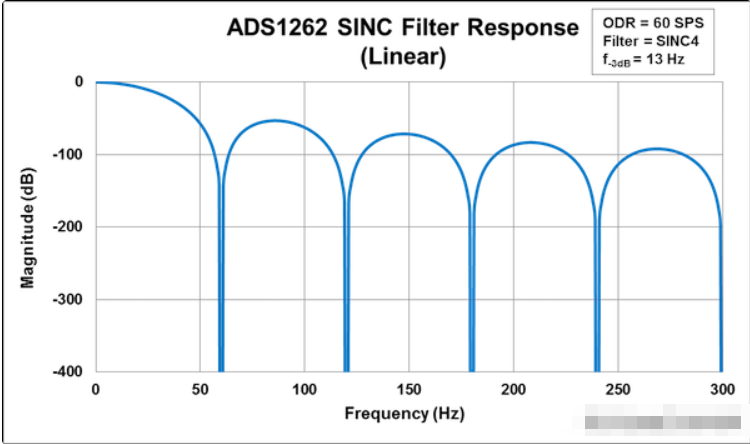
图3 ADS1262 SINC滤波器响应-线性频标，f最大值=300Hz

这两个滤波器响应图之间的一个细微但重要的区别是sinc滤波器图（图3）使用线性频率轴，而抗混叠滤波器图（图2）具有对数频率轴。这种差异是由于大多数delta-sigma adc的数据传输速度慢造成的，在这种情况下，通常不需要显示多个频率的几十年。不幸的是，这种选择使将滤波器组合到同一个图中的过程复杂化。

另外，回想一下sinc滤波器的响应会无限期地重复——它并不像图3中所示的那样在300Hz时简单地“停止”。

如果考虑到这两个问题，并在更宽的频率范围内以对数轴绘制sinc滤波器响应，则图4中的结果与大多数ADC数据表中的典型曲线图非常不同。

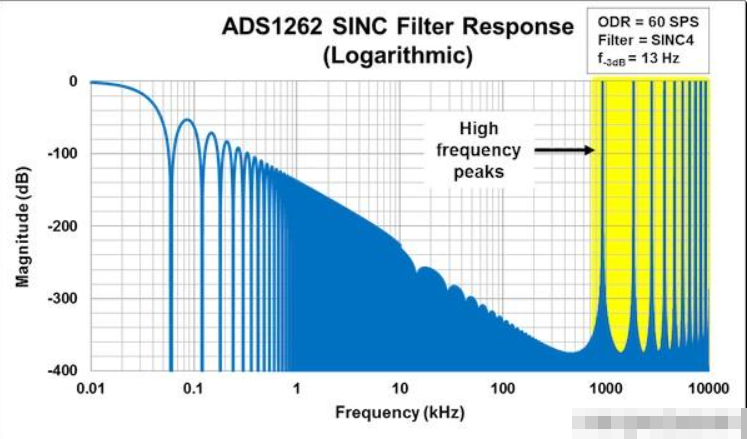
图4 ADS1262 SINC滤波器响应-对数频标，f最大值=10MHz

将对数轴绘制成10MHz，您现在可以看到高频峰值，指示滤波器响应重复。为什么这很重要？由于这种重复，在sinc滤波器的频率响应曲线下积分产生无穷大的ENBW（从数学角度来看，sinc滤波器的积分在无穷远处发散）。图5描绘了抗混叠和sinc滤波器频率响应以及它们各自的enbw的曲线图。

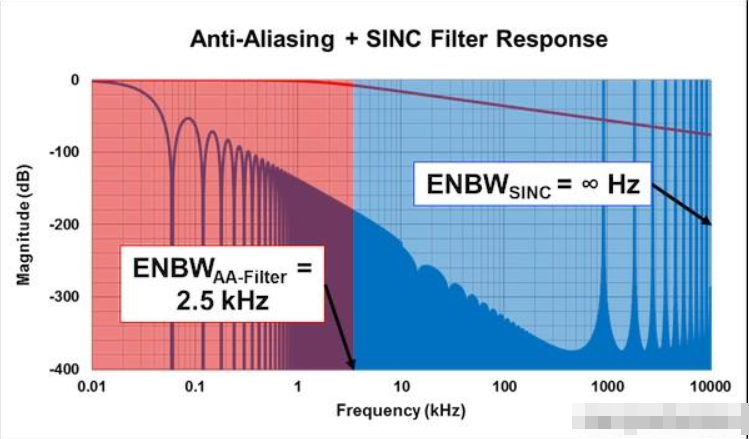
图5 SINC和抗混叠滤波器的ENBWs

在sinc滤波器无限大的ENBW下，如何继续这个分析？您只需设置集成的限制。通常，调制器时钟频率（fMOD）的某些倍数（1或2）是可以接受的，但是在这种情况下，可以使用抗混叠滤波器作为限制。

既然这两个滤波器都是具有相同x轴刻度的震级图（以分贝（dB））为单位），您可以简单地将它们相加，以确定整个系统的ENBW。这就产生了图6所示的滤波器响应。综合RC和数字滤波器的组合响应现在可以得到14Hz的ENBW，比任何一个滤波器本身都小几个数量级。

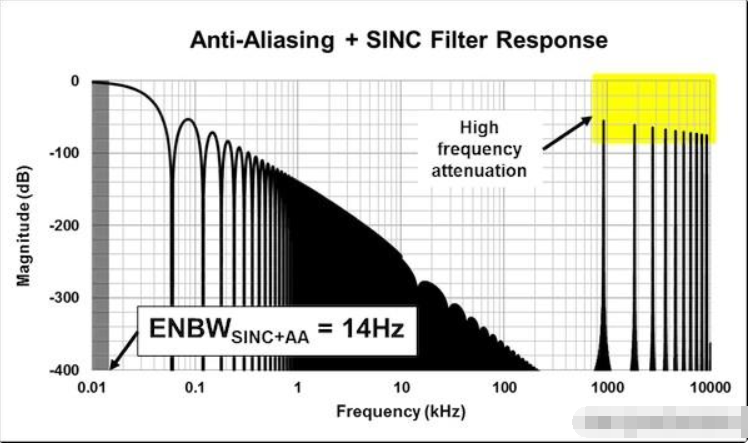
图6 SINC和抗混叠滤波器的系统响应

窄的ENBW是由于抗混叠滤波器在较高频率下衰减sinc滤波器的噪声功率，从而使进入系统的噪声更小。这也进一步解释了为什么不需要考虑sinc滤波器的无限频率响应。抗混叠滤波器已经消除了许多与fMOD倍数出现的高频峰值相关的噪声功率否则折叠回通带. 许多模拟设计人员假定抗混叠滤波器的预期目的是去除低频噪声，这通常是delta-sigma模数转换器的数字滤波器 .

如果你遵循这个假设设计一种抗混叠滤波器对于一个非常低的截止频率，你通常需要使用大的电阻和电容值。然而，较大的无源分量值会导致较长的信号稳定时间，这通常是您希望避免的。即使您可以接受一个额外的稳定时间，ADC输入泄漏电流也会在大的滤波器电阻上引起显著的偏移电压，从而导致系统级的不准确。因此，您只需要为高频噪声设计抗混叠滤波器，因为较小的无源元件可以帮助避免上述问题，这实际上对系统有利。

假设现在要更改ADC的采样率或抗混叠滤波器的截止频率。这对系统ENBW有何影响？直观地说，具有较小截止值的滤波器将主导ENBW计算是有意义的——正如我已经展示的那样——这通常是正确的。为了说明这一点，表2列出了ADS1262的所有可用数字滤波器输出数据速率，以及一系列抗混叠截止频率的相应系统ENBW。表2还提供了ADC的3dB点，它有效地充当了它的截止频率。

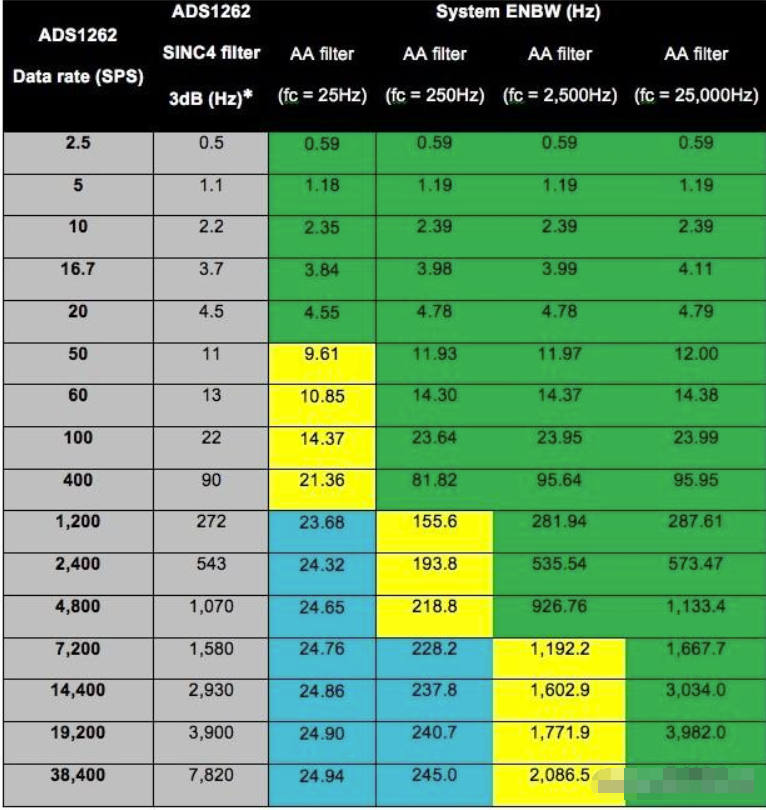
表2 ADC数据速率和AA滤波器截止频率对系统ENBW的影响。

注：结果来自ADS1262计算器工具。

表2中突出显示的部分表示以下情况：

绿色=系统的ENBW在ADC 3dB点的10%以内。

蓝色=系统的ENBW在抗混叠滤波器截止频率的10%以内。

黄色=系统的ENBW不在抗混叠滤波器截止频率的ADC 3dB点的10%以内。

系统ENBW和单个滤波器截止点之间的这些关系允许您近似系统ENBW，而不是执行复杂的积分，假设等式2和3中表示的条件之一是真的：

如果两个条件都不成立，那么f3分贝（ADC）f相对接近c（AA过滤器），则有必要执行本节概述的集成。此外，这些条件通常也适用于任何数量的附加滤波器级，只要它们的截止频率远大于ADC或抗混叠滤波器的截止频率。在这种情况下，你不必计算他们的enbw，这样分析就不那么复杂了。

在“解析信号”系列的下一篇文章中，我将通过在信号链中添加集成和外部放大器来继续讨论delta-sigma adc中的噪声。

以下是一些要点的总结，有助于更好地理解delta sigma adc中的ENBW：

• ENBW通常由具有最小截止频率的滤波器控制，该滤波器通常是抗混叠滤波器或数字滤波器，特别是对于精密的delta-sigma adc。

• 抗混叠滤波器用于去除高频噪声，而非低频噪声。

• 您可以使用直接积分来计算ENBW，或者在大多数情况下使用ADC的3dB点或抗混叠滤波器的截止频率来近似它。

*博客内容为网友个人发布，仅代表博主个人观点，如有侵权请联系工作人员删除。